11153. Кефа и парк

Кефа решил отпраздновать свой первый крупный заработок походом в ресторан.

Он живет рядом с необычным парком, который представляет собой подвешенное дерево из n вершин c корнем в вершине 1. В вершине 1 также находится дом Кефы. К сожалению для нашего героя, в парке обитают коты, и Кефа уже выяснил номера вершин, в которых они находятся.

Рестораны расположены в листовых вершинах парка. Кефа хочет выбрать ресторан, но он очень боится котов. Поэтому он ни за что не пойдёт в ресторан, если на пути к нему от его дома встретится более m подряд идущих вершин с котами.

Ваша задача – помочь Кефе посчитать количество ресторанов, в которые он может безопасно пойти.

Вход. В первой строке заданы два целых числа n и m (2 ≤ n ≤ 10⁵, 1 ≤ m ≤ n) – количество вершин дерева и максимальное количество подряд идущих вершин с котами, которое Кефа способен перенести.

Во второй строке содержится n целых чисел a₁, a₂, ..., a_n, где каждое a_i равно либо 0 (в вершине i нет кота), либо 1 (в вершине i есть кот).

В следующих n – 1 строках перечислены ребра дерева в формате x_i y_i (1 ≤ x_i, y_i ≤ n, x_i ≠  y_i), где x_i и y_i – вершины дерева, соединенные очередным ребром.

Гарантируется, что данный набор рёбер задаёт дерево.

Выход. Выведите количество листьев дерева, до которых Кефа сможет добраться, если на пути от его дома встречается не более m подряд идущих вершин с котами.

Пример входа 1	Пример выхода 1
7 1 1 1 0 0 0 0 1 1 2 1 3 2 4 2 5 3 6 3 7	2
Пример входа 2	Пример выхода 2
8 2 1 1 0 1 0 1 0 1 1 2 2 3 2 5 2 6 3 4 6 7 6 8	2

РЕШЕНИЕ

дерево

Анализ алгоритма

Запустим поиск в глубину из вершины 1, где находится дом Кефы. В одном из параметров функции dfs будем хранить количество подряд идущих вершин с котами. Если в вершине v это число превысит m, дальнейший поиск в глубину из этой вершины не выполняем. Подсчитываем количество посещенных листьев. Вершина является листом, если ее степень равна 1 и при этом она не является корнем (то есть вершиной 1).

Пример

Рассмотрим деревья из первого и второго примеров.

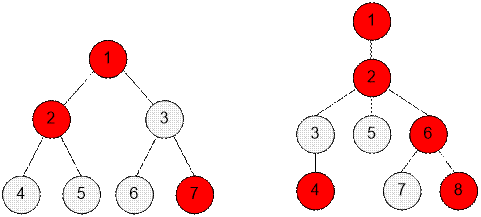
В первом примере Кефа может пройти подряд только через одну вершину с котом. Он сможет попасть в рестораны, расположенные в вершинах 6 и 7.

Во втором примере Кефа может пройти подряд только через две вершины с котами. Он сможет попасть в рестораны, расположенные в вершинах 4 и 5.

Реализация алгоритма

Расположение котов храним в массиве cats. Дерево храним в списке смежности g.

vector<int> cats;

vector<vector<int> > g;

Функция dfs выполняет поиск в глубину из вершины v и возвращает количество ресторанов, до которых можно добраться из этой вершины (при условии что на пути к ним встречается не более m подряд идущих вершин с котами). Предком вершины v является вершина prev. Количество подряд идущих вершин с котами, пройденных вплоть до вершины v включительно, равно cnt.

int dfs(int v, int prev, int cnt)

{

Если уже пройдено более m котов подряд, то дальнейший поиск в глубину из вершины v не продолжается.

if (cnt > m) return 0;

Если мы находимся в листе, то увеличиваем количество ресторанов, в которые можно попасть.

if (g[v].size() == 1 && prev != -1) return 1;

В переменной res подсчитываем количество ресторанов, достижимых из вершины v.

int res = 0;

Перебираем все ребра (v, to), исходящие из v. Если вершина to является предком v, то не совершаем переход в эту вершину.

for (int to : g[v])

if (to != prev)

{

Если в вершине v нет кота, устанавливаем c = 0. В противном случае присваиваем c = cnt + 1. Переменная c хранит количество подряд идущих вершин с котами до вершины to включительно.

int c = (cats[to] == 0) ? 0 : cnt + 1;

Запускаем поиск в глубину из вершины to.

res += dfs(to, v, c);

}

Возвращаем результат.

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d", &n, &m);

cats.resize(n + 1);

for (i = 1; i <= n; i++)

scanf("%d", &cats[i]);

Строим дерево.

g.resize(n + 1);

for (i = 1; i < n; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

Выводим ответ. Функция dfs, вызванная из вершины 1, возвращает ответ на задачу. Поскольку у вершины 1 нет предка, вторым параметром передадим значение -1. Стартовав из вершины 1, мы посетили cats[1] котов.

printf("%d\n", dfs(1, -1, cats[1]));

Python реализация

Функция dfs выполняет поиск в глубину из вершины v и возвращает количество ресторанов, до которых можно добраться из этой вершины (при условии что на пути к ним встречается не более m подряд идущих вершин с котами). Предком вершины v является вершина prev. Количество подряд идущих вершин с котами, пройденных вплоть до вершины v включительно, равно cnt.

def dfs(v, prev, cnt):

Если уже пройдено более m котов подряд, то дальнейший поиск в глубину из вершины v не продолжается.

if cnt > m:

return 0

Если мы находимся в листе, то увеличиваем количество ресторанов, в которые можно попасть.

if len(g[v]) == 1 and prev != -1:

return 1

В переменной res подсчитываем количество ресторанов, достижимых из вершины v.

res = 0

Перебираем все ребра (v, to), исходящие из v. Если вершина to является предком v, то не совершаем переход в эту вершину.

for to in g[v]:

if to != prev:

Если в вершине v нет кота, устанавливаем c = 0. В противном случае присваиваем c = cnt + 1. Переменная c хранит количество подряд идущих вершин с котами до вершины to включительно.

c = 0 if cats[to] == 0 else cnt + 1

Запускаем поиск в глубину из вершины to.

res += dfs(to, v, c)

Возвращаем результат.

return res

Основная часть программы. Читаем входные данные.

n, m = map(int, input().split())

cats = [0] + list(map(int, input().split()))

Строим дерево.

g = [[] for _ in range(n + 1)]

for _ in range(n - 1):

a, b = map(int, input().split())

g[a].append(b)

g[b].append(a)

Выводим ответ. Функция dfs, вызванная из вершины 1, возвращает ответ на задачу. Поскольку у вершины 1 нет предка, вторым параметром передадим значение -1. Стартовав из вершины 1, мы посетили cats[1] котов.

print(dfs(1, -1, cats[1]))